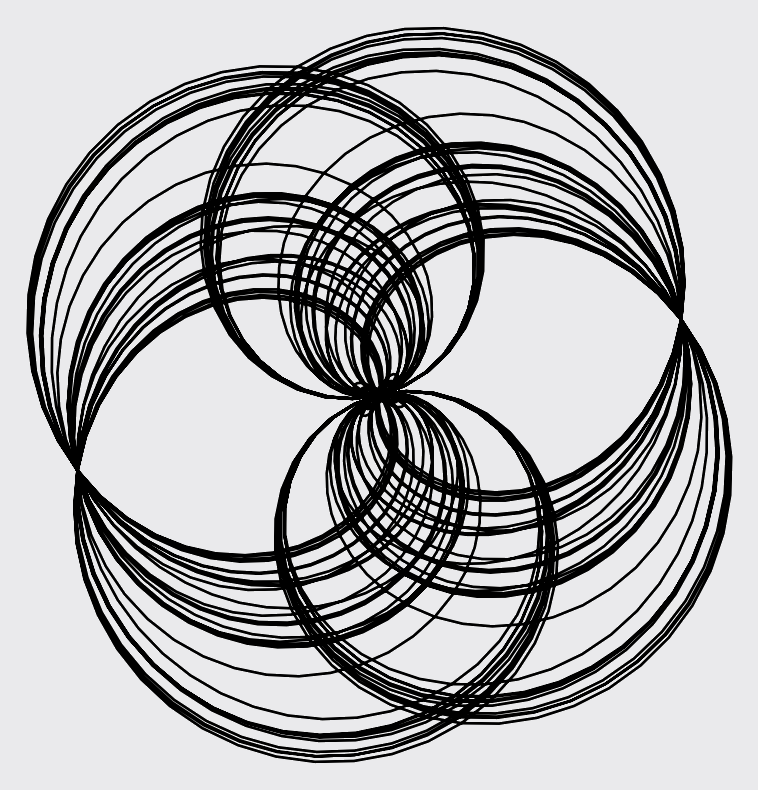Dirichlet Characters
In mathematics, a character is a well-behaved function from a group to a field. In number theory, the most common characters are Dirichlet characters, which are functions from the integers to the unit circle.
More precisely, a Dirichlet character \(\chi\) is a multiplicative function $$ \chi : (\mathbb{Z}/N\mathbb{Z})^\times \longrightarrow \mathbb{C}. $$
Every Dirichlet character has a label consisting of two integers, \(N\) and \(a\). The character \(\chi(N, a)\) (sometimes written \(\chi_N(a, \cdot)\)) is defined modulo \(N\) and has index \(a\).
The idea of plotting a Dirichlet character is a bit odd, since the "image" consists of several points on the unit circle. These plots would highly resemble various approximations of the circle --- mostly uninteresting. But a character can be interpolated to a function \(\chi : \mathbb{R} \longrightarrow \mathbb{C}\) through a Gauss sum $$ \tau(\chi) := \sum_{n \bmod N} \chi(n) \exp(2 \pi i n / N). $$ One can prove the identity $$ \chi(x) = \frac{\chi(-1) \tau(\overline{\chi})}{N} \sum_{n \bmod N} \overline{\chi}(n) \exp(2 \pi i n x / N), $$ and note that this function makes sense for all \(x \in \mathbb{R}\). On integers, it agrees with the typical Dirichlet character.
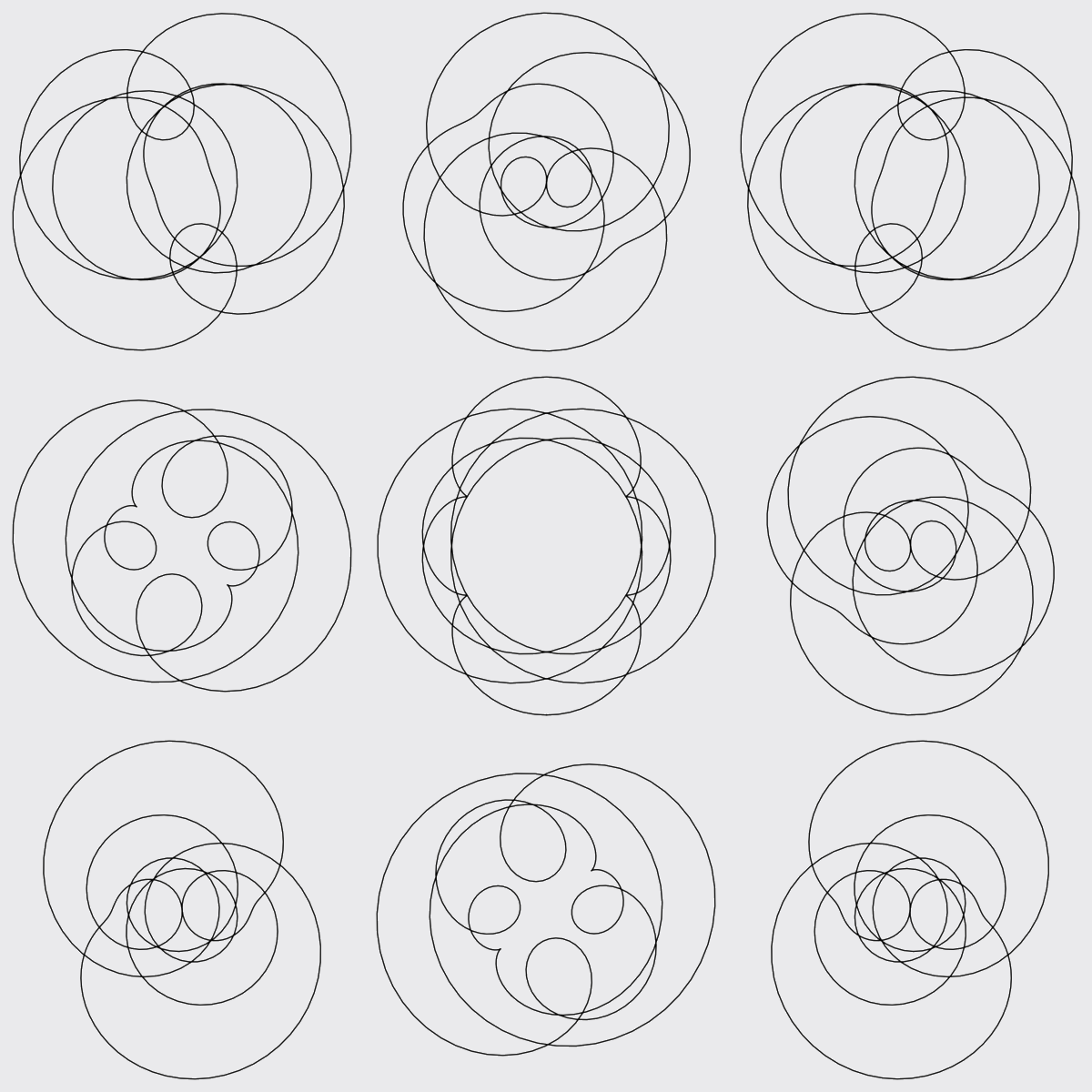
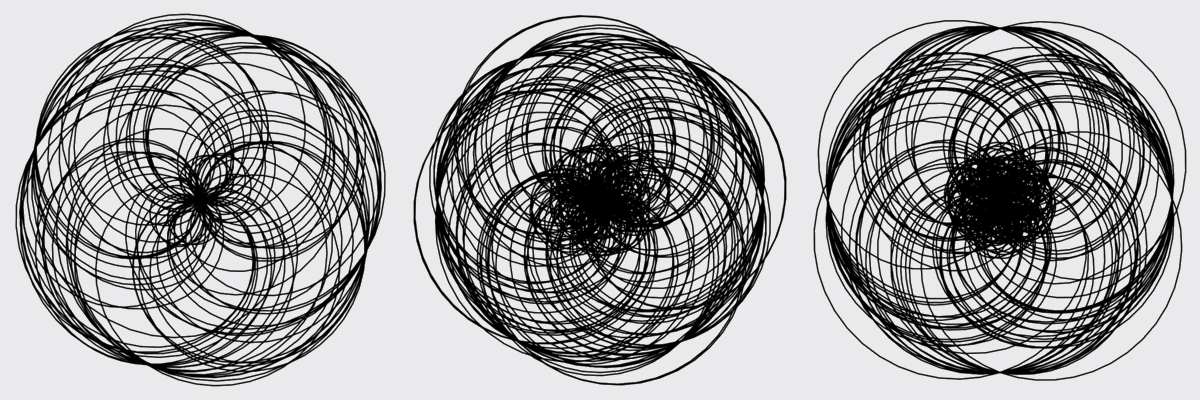
Now it is possible to plot many characters. These are the characters mod \(22\), excluding the trivial character.
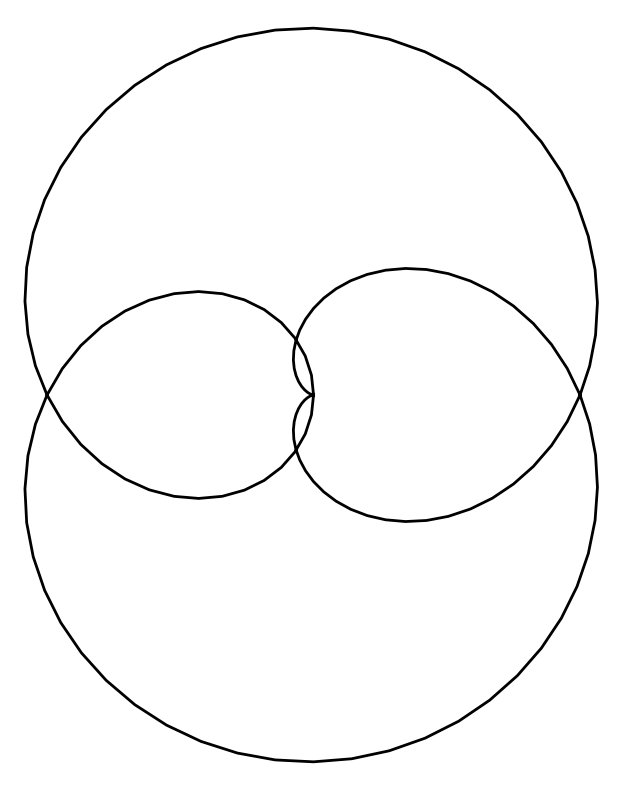
Some characters look very simple.
Others look more complicated.
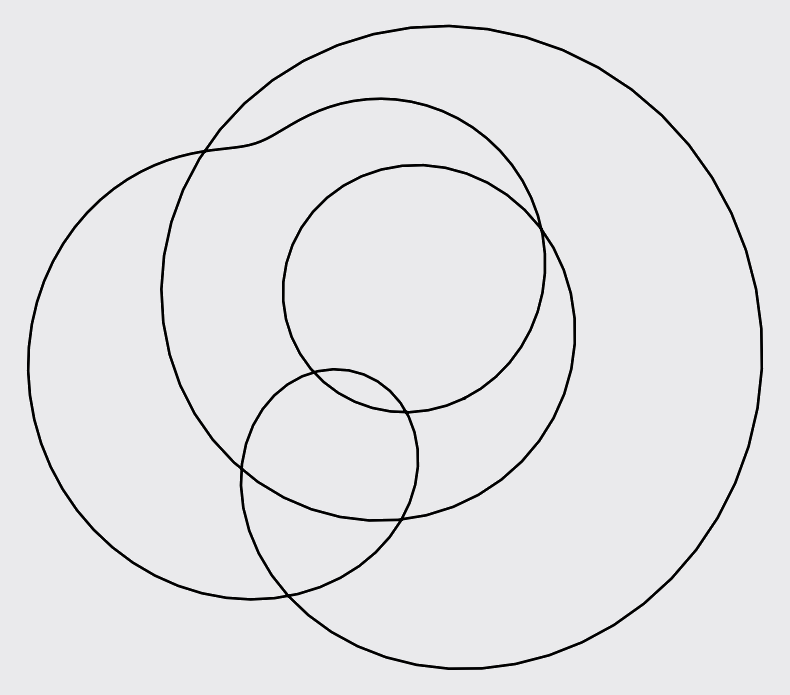
Others look downright busy.
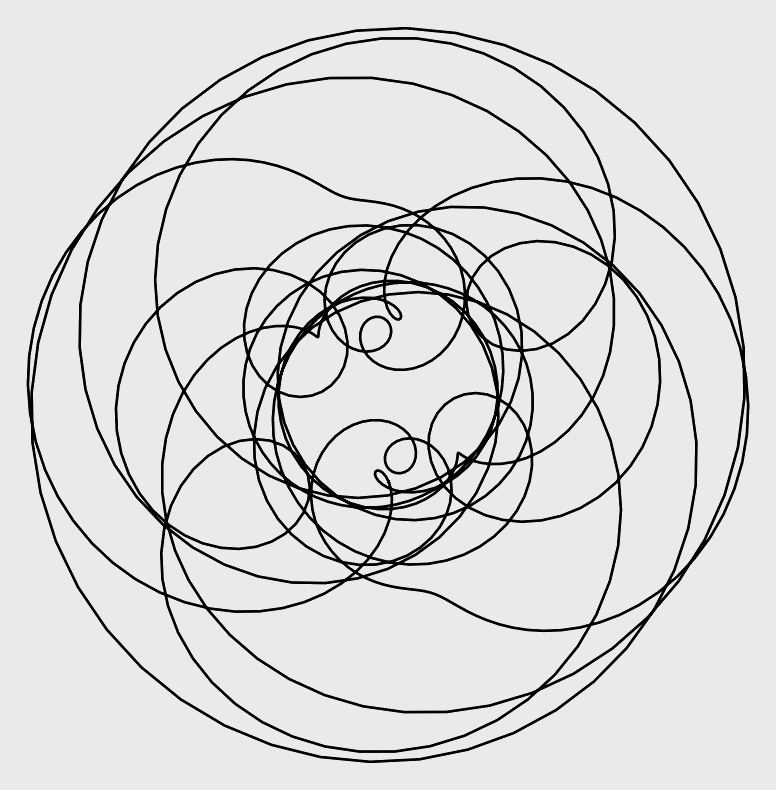
But as one continues to make and study these images, patterns emerge. A curtain hides an underlying image --- subsequent characters shed light, but the image remains obscured.
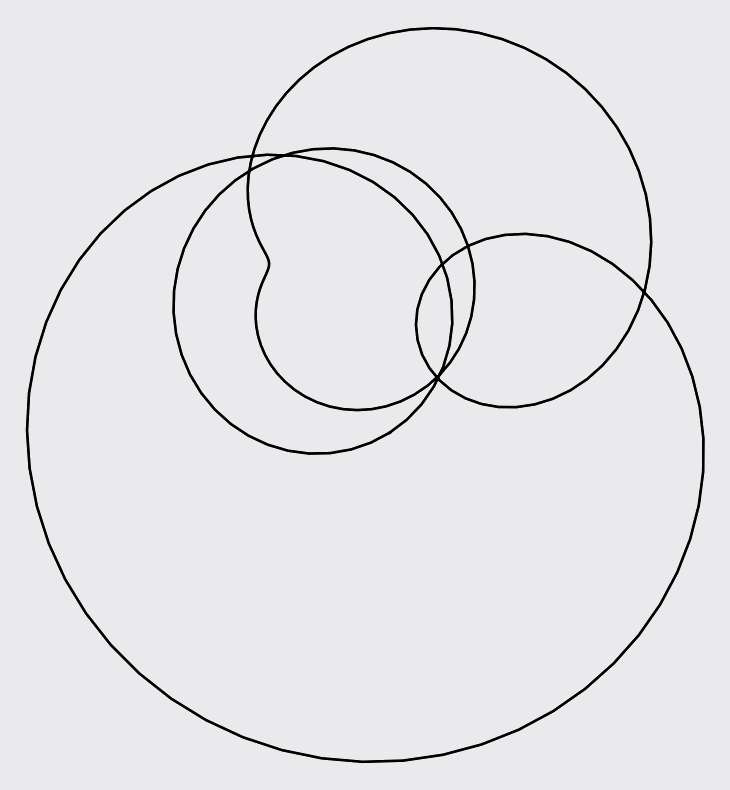
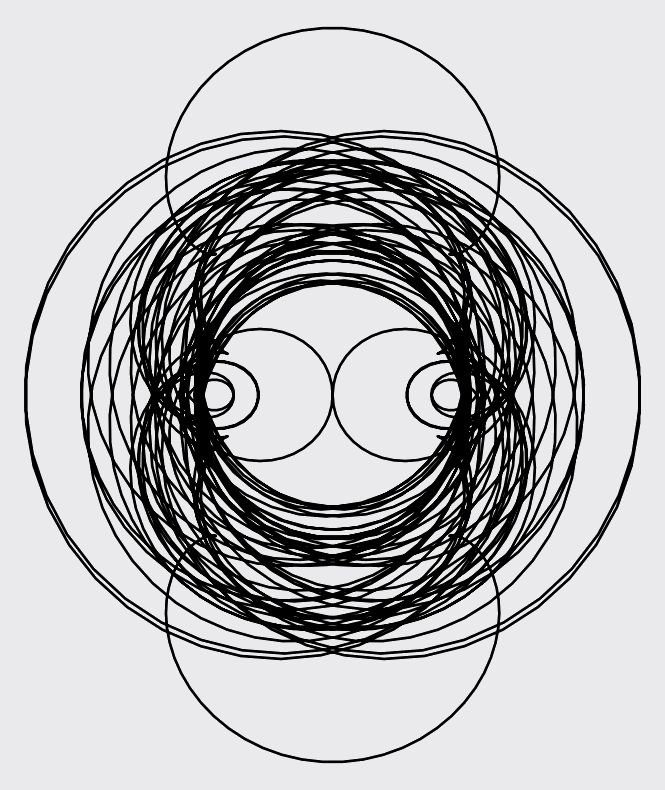
Or there may be a feeling like someone is watching you.
Even the busy character above seems to be one part in a sequence. The next term might look like the following.

For characters with larger moduli, the images take on a different facet of beauty.
The clustering around the center and around an apparent circle are not coincidental. At integer inputs $n$, $\chi(n)$ will either be $0$ or lie on the unit circle. In many images, the tension comes from the the apparent randomness and the need to return to the circle.
Prints of high-res versions of these images are available. Contact me at mixedmathart@lowryduda.com for more.