mixedmathart

Modular Forms

My PhD, and most of my research, is centered on the topic of modular forms. Recently I began to study their visualizations.

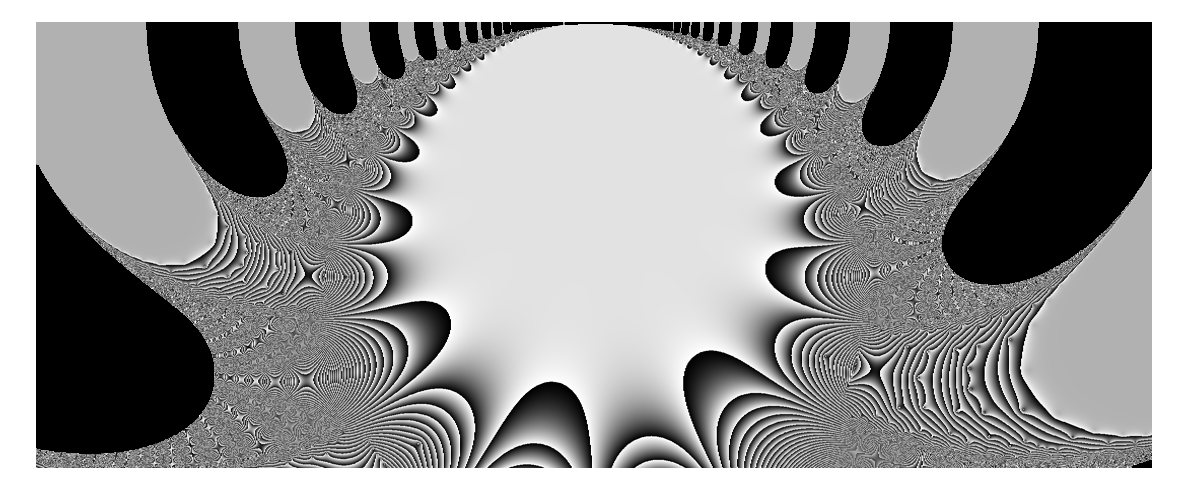
A modular form \(f(z)\) on \(\mathrm{GL}(2)(\mathbb{R})\) is a complex-valued function that is highly self-symmetric. This can be made rigorous, but the idea is that the values of the function in one area are essentially related to the values in many other areas.

Image of the delta function on the disk
$\Delta(z)$ in grey. DLD Sept 2020.
Image of the delta function
$\Delta(z)$ on the disk in grey. DLD Sept 2020.

In pictures, this manifests as patterns that seem to repeat, or nearly repeat.

There is a profound challenge to visualizing these objects. They are naturally four dimensional. How are we to see one?

Image of 105.2.a.a on the disk
$f_{105}$ in grey on the disk. DLD Sept 2020.
Image of 105.2.a.a
$f_{105}$ in grey. DLD Sept 2020.

Mathematicians frequently use a combination of color and brightness to represent the two dimensions of the output of a complex-valued function. The result can be dazzling, but often the result is very noisy.

Here I deliberately avoid color. I do this not because it's better, but because it's already enough to see the self-symmetry. It's already beautiful.

Image of 10.20.a.a on the disk
Features in the mist i. DLD Sept 2020.
Image of 10.20.a.a
Features in the mist ii. DLD Sept 2020.

Even without color, it is possible to draw attention to self-similarity. By cycling through shades of grey, we produce a graduated contour map. Shapes emerge, peaks, troughs, valleys --- or perhaps layers of a conch, or rippled sand in a desert.

Image of 105.2.a.a on the disk
Cyclic $f_{105}$ on the disk. DLD Sept 2020.
Image of 105.2.a.a
Cyclic $f_{105}$ on the disk. DLD Sept 2020.

Each modular form has a natural domain: the upper half plane, consisting of pairs \((x, y)\) of real numbers with \(y > 0\) (or as the complex numbers \(x + iy\) with \(y > 0\)). In half of the images here, I map the upper half plane to a disk, and instead show the disk.

The map I use from the plane to the disk is distinguished. Circles and straight lines in the plane appear as different circles and straight lines in the disk. The line \(y = 0\) in the plane is mapped to the circle \(x^2 + y^2 = 1\), and the line \(x = 0\) in the plane is mapped to itself.

Image of 10.20.a.a on the disk
Cyclic $f_{10}$ on the disk. DLD Sept 2020.
Image of 10.20.a.a
Cyclic $f_{10}$. DLD Sept 2020.

Thus the bottom center of two images will appear very similar, but the similarities will become more and more distorted away from the bottom center. But both are honest.

Fisheye image of 10.20.a.a
$f_{10}$ through a fisheye i. DLD Sept 2020.
Fisheye Image of 10.20.a.a
$f_{10}$ through a fisheye ii. DLD Sept 2020.

By choosing different maps that are less truthful, we see different views of the modular form. This is like looking at a picture taken from a fish-eye lens.

Fisheye image of 10.20.a.a
$f_{10}$ through a fisheye iii. DLD Sept 2020.
Fisheye image of 10.20.a.a
$f_{10}$ through a fisheye iv. DLD Sept 2020.
Fisheye image of 10.20.a.a
$f_{10}$ through a fisheye v. DLD Sept 2020.
Fisheye image of 10.20.a.a
$f_{10}$ through a fisheye vi. DLD Sept 2020.
Fisheye image of 10.20.a.a
$f_{10}$ through a fisheye vii. DLD Sept 2020.
Fisheye image of 10.20.a.a
$f_{10}$ through a fisheye viii. DLD Sept 2020.