Modular Form ii

This is a continuation of ideas from before, except we now embrace color. But we don't use the typical colors.

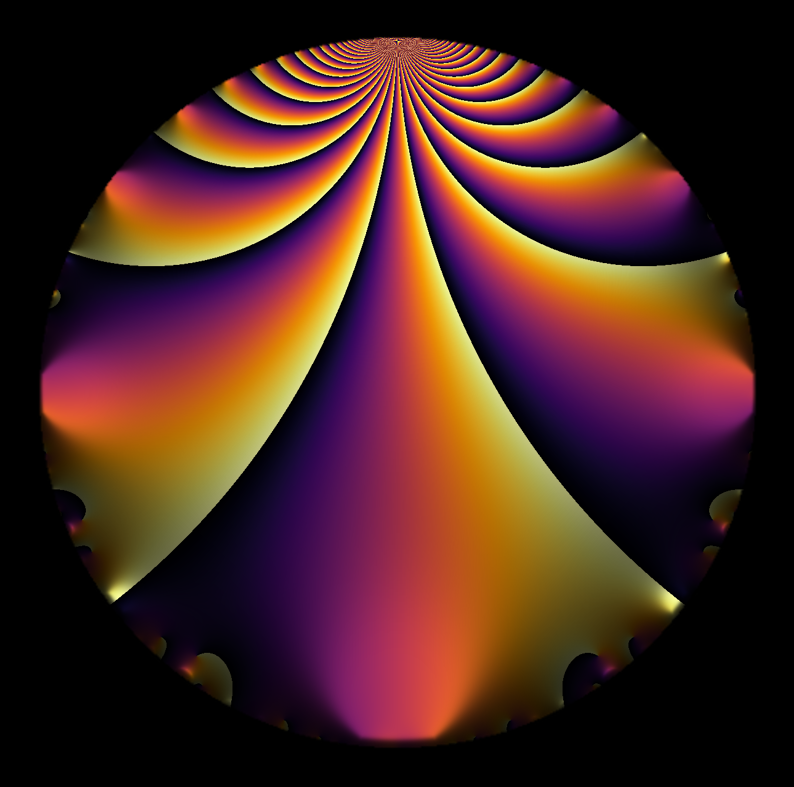
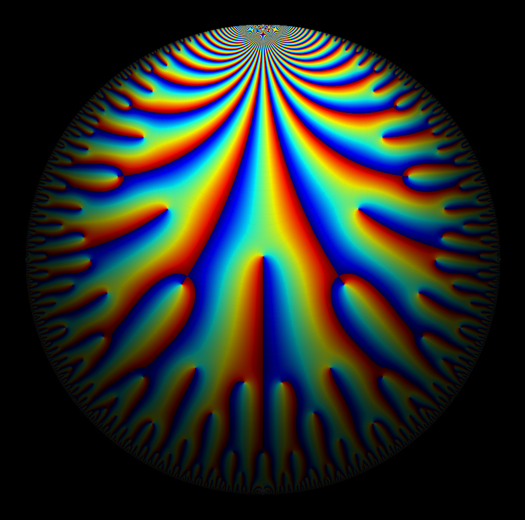
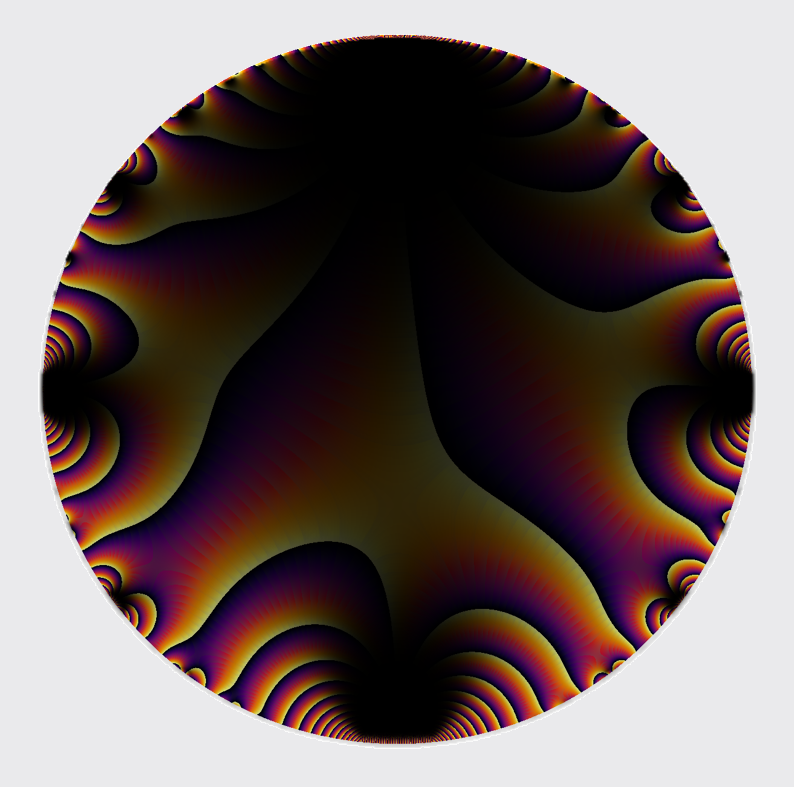
A complex-valued function \(f: \mathbb{C} \longrightarrow \mathbb{C}\) naturally has a four dimensional graph. We represent this in two dimensions here by representing each point \(z\) in the codomain by \(z = r e^{i \theta}\), for a magnitude \(r\) and argument \(\theta\). Here, we choose colors based on \(\theta\), and we encode the magnitude in a variety of ways.

Sometimes we use contours in indicate the magnitude.

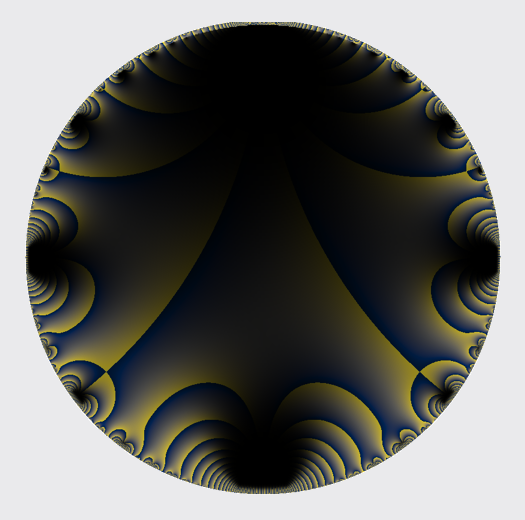
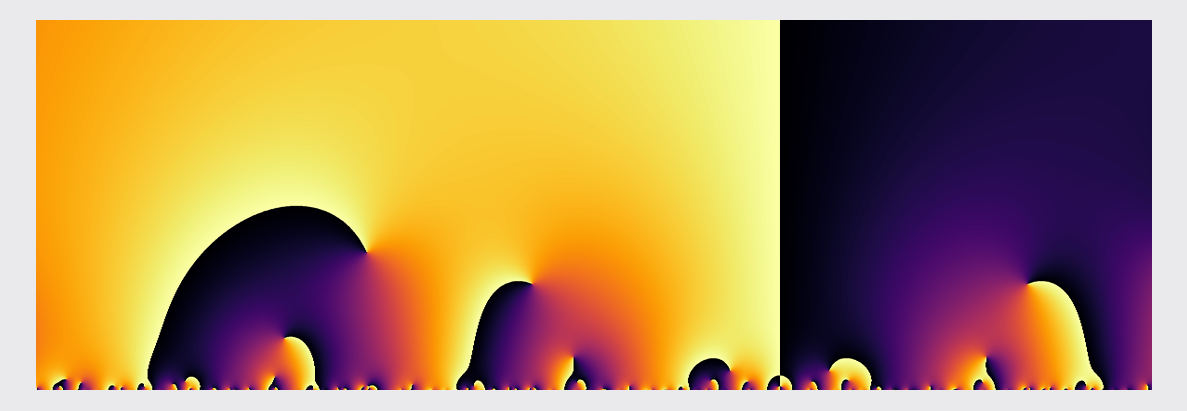
Or we use darkness or lightness to indicate the magnitude.

Choosing small windows, various forms of self-similarity make themselves obvious. These images have a flow much like the surface of a stream. Colors swirl in eddies and whirlpools.

Small differences in color can have strong associative effect. The following image is essentially the same as Features in the mist i, from before, but with colors inverted and on a grey paper background.

This is a modular form, but it looks like a speckled marble, perhaps a solar map.